Introduction

The scaling laws for neural language models showed that cross-entropy loss follows a power law in three factors:

  1. Dataset size
  2. Model parameters
  3. Training compute (steps or epochs)

The lower the cross-entropy loss, the better the model’s next-token prediction. Since prediction and compression are deeply linked (The Intricate Link Between Compression and Prediction), a lower loss should translate into better lossless compression. This raises the question:

Do LLMs exhibit clean power-law scaling in compression performance?

Experiment

For the experiment, I considered the Pythia models, which are available at multiple checkpoints and parameter sizes. All Pythia models are trained on the same dataset (The Pile), ensuring a uniform comparison. Following Delétang et al. (2023), The LLM’s predicted probabilities for each token are used to update the symbol table of an arithmetic encoder (a near-optimal entropy coder). I took the first 2048 chunks of the enwik8 dataset each chunk is 2048 bytes and fed them to the LLM to predict the next-token probabilities.

The other experimental parameters are:

  • Models: EleutherAI Pythia family (8-bit quantized): 70 M, 160 M, 410 M, 1 B, 1.4 B parameters
  • Checkpoints: 1 k, 8 k, 32 k, 128 k, 143 k training steps
  • Chunking:
    • CHUNK_SIZE: 2048 bytes
    • NUM_CHUNKS: 2048 per dataset
  • Compression pipeline:
    1. Raw bytes → ASCII
    2. Tokenize and pass the ASCII symbols to LLM
    3. Arithmetic coding on LLM probabilities
    4. CR = compressed_bits / original_bits
  • Datasets & Preprocessing:
    • Text: enwik8 (Wikipedia XML)
    • Image: ImageNet-1k validation → 32 × 64 grayscale patches (uint8 bytes)
    • Speech: LibriSpeech “clean” train.100 → 16 kHz PCM → int16 bytes

Results: Text Compression

Model 1 k 8 k 32 k 128 k 143 k
pythia-70M 0.223 0.176 0.17 0.173 0.175
pythia-160M 0.218 0.159 0.149 0.149 0.150
pythia-410M 0.223 0.148 0.136 0.129 0.128
pythia-1B 0.207 0.140 0.128 0.120 0.120
pythia-1.4B 0.207 0.137 0.124 0.115 0.115

Text scaling-law fit

We fit a Kaplan-style power law
\(\mathrm{CR}(P,S) = a + b\,P^{-\alpha} + c\,S^{-\beta}.\)
For text, the best-fit coefficients are:
\(\mathrm{CR}_{\text{text}} = 0.10 + 60\,P^{-0.38} + 10\,S^{-0.75}.\)

Compression on Non-Text Modalities

The “Language Modeling Is Compression” paper shows that an LLM trained only on text can compress arbitrary byte streams Language Modeling Is Compression. I applied the same pipeline to ImageNet-1k patches and LibriSpeech audio.

Image Results

Model 1 k 8 k 32 k 128 k 143 k
pythia-70M 0.601 0.499 0.492 0.505 0.513
pythia-160M 0.615 0.483 0.471 0.482 0.492
pythia-410M 0.668 0.506 0.461 0.444 0.447
pythia-1B 0.601 0.470 0.456 0.436 0.440
pythia-1.4B 0.643 0.482 0.470 0.434 0.436

Image scaling-law fit

\[\mathrm{CR}_{\text{image}} = 0.38 + 2\,P^{-0.15} + 60\,S^{-0.86}.\]

Speech Results

Model 1 k 8 k 32 k 128 k 143 k
pythia-70M 0.695 0.460 0.439 0.475 0.466
pythia-160M 0.678 0.440 0.430 0.433 0.456
pythia-410M 0.770 0.505 0.404 0.383 0.391
pythia-1B 0.677 0.424 0.444 0.376 0.384
pythia-1.4B 0.752 0.469 0.443 0.378 0.385

Speech scaling-law fit

\[\mathrm{CR}_{\text{speech}} = 0.39 + 8\times10^{3}\,P^{-0.68} + 1\times10^{2}\,S^{-0.85}.\]

Combined Scaling Curves

The below plot shows the overall scaling laws plots across all the three modalities, While the scaling law trend is present in non-textual modalities, the compression is not as strong in text.

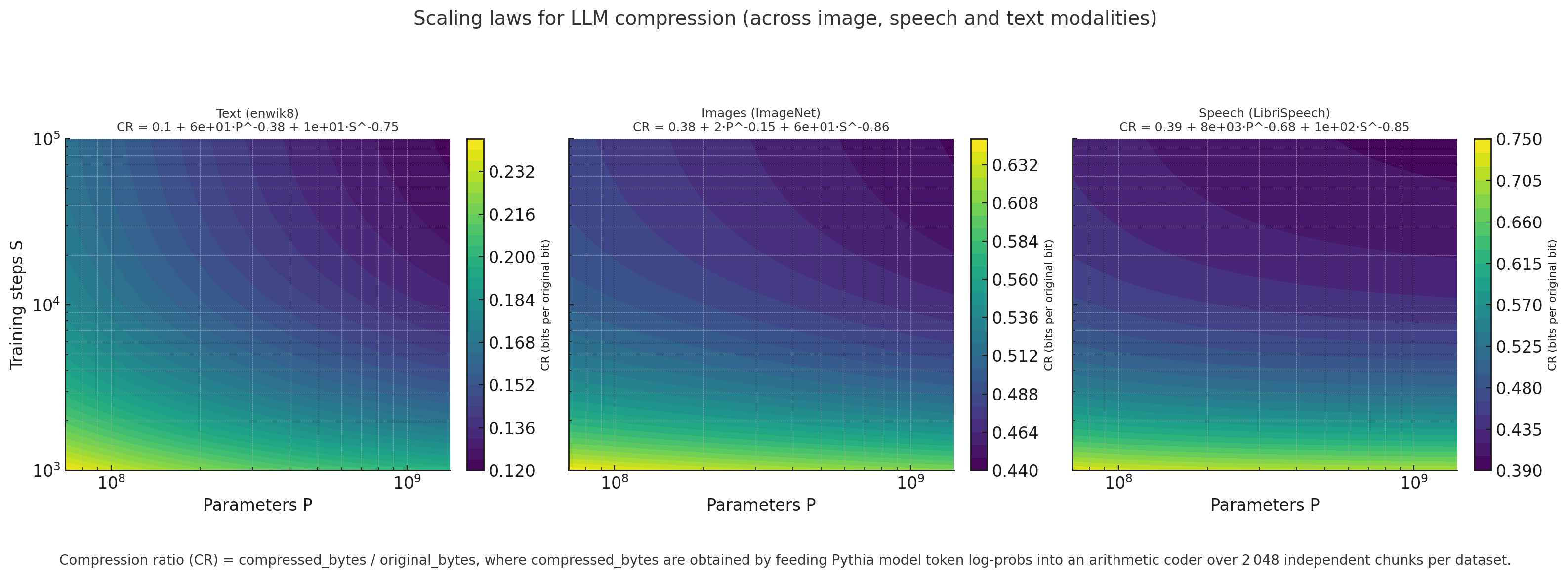
Scaling curves for text, image, speech

Conclusion

It has been argued that LLMs trained only on text can form world models for proto-AGI. These compression results reinforce that claim: despite text-only pretraining, LLMs compress images and speech following clear power laws.

We hypothesize two primary mechanisms responsible for this:

  1. In-Context Learning
    Within a given token window, self-attention adapts on-the-fly to file-specific patterns (repeating pixels, periodic audio cycles), shaving off most of the entropy.

  2. Universal Sequence Prior
    Pretraining internalizes bursty repetitions, Zipf’s law, heavy tails, and long-range autocorrelations statistics shared by all byte streams. Even without context, compression ratio should be far below uniform-noise rates. Do read Benford’s Law, Zipf’s Law and the Pareto Distribution to know more about naturally occuring data distributions and their universality

A really interesting future work should be to quantify each component’s contribution and trace how they emerge during pretraining.

References