Experiments with the Platonic Representation Hypothesis
Introduction
The Platonic Representation Hypothesis (PRH) suggests that neural networks, despite being trained with different objectives and on various modalities, converge to a shared statistical understanding of reality. Inspired by Plato’s Allegory of the Cave, PRH posits that models across domains—such as vision and language—internalize similar structures, reflecting an idealized model of the world. While initial experiments focused on image-based models like Vision Transformers (ViT) trained on the same pretraining dataset (ImageNet), this raises an important question:
Does PRH hold only when models are trained on data from the same distribution?
To evaluate PRH beyond in-distribution data, I extended experiments to three scenarios:
- In-distribution data: Utilized the validation set from Places365, aligning closely with the training data of many vision models.
- Out-of-distribution (OOD) data: Employed the ImageNet-O dataset, containing images that diverge significantly from the standard ImageNet distribution.
- Random noise: Generated purely random images to probe the extreme boundaries of representational alignment.
Results:
In-Distribution Setting
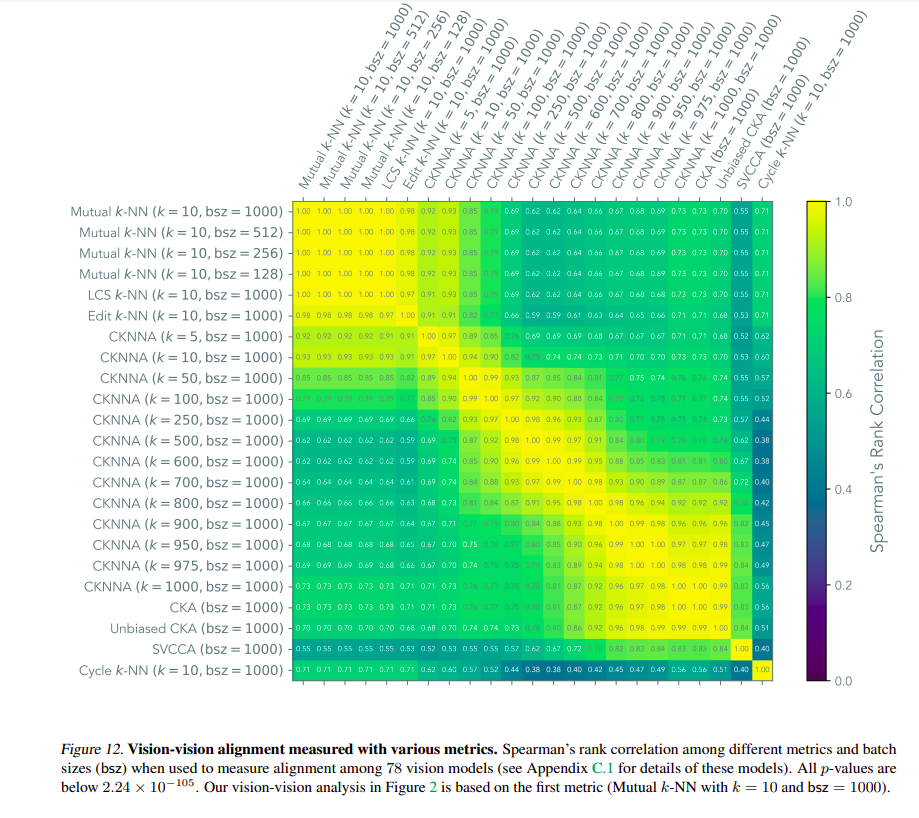
Figure 1: Spearman rank correlation between models on Places365’s validation data, indicating a high degree of alignment in in-distribution data. This graph is straight from the platonic-representation-hypothesis paper. The ViT models used in this experiment are trained more or less on the same data distribution/pretraining datasets.
Out-of-Distribution Data
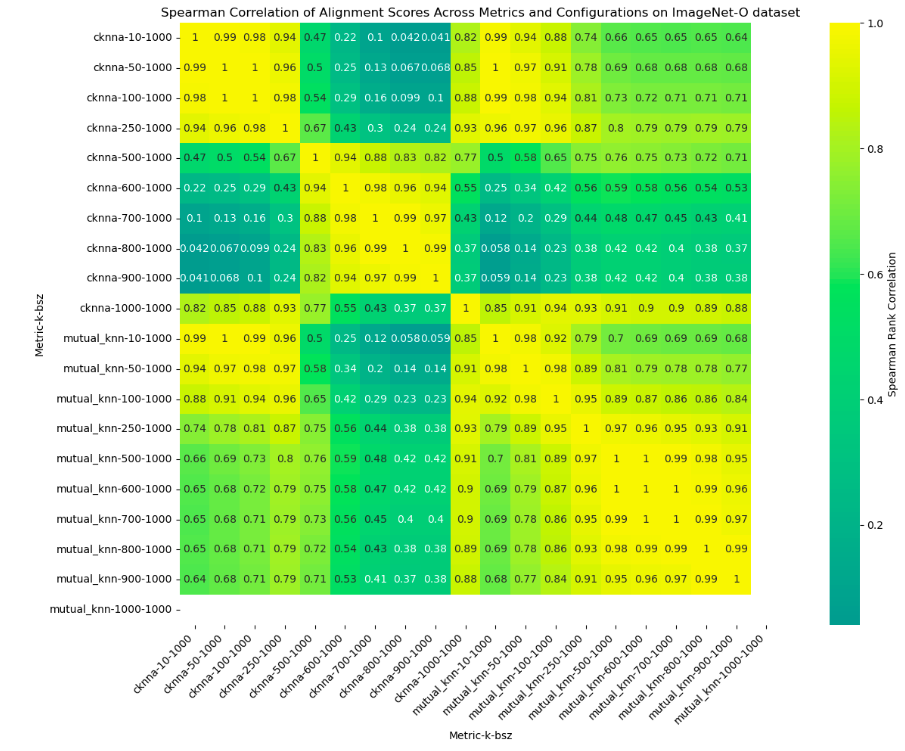
*Figure 2: Alignment of vision models on the ImageNet-O dataset. Spearman correlation suggests that even with OOD data, models maintain a shared statistical representation, models converge in their representations, implying PRH still holds true and generalizes well outside the training distribution of the model’s training set. This fact has really good implications in understanding failure models and alignment failures of models belonging to same architectural family
Random Noise Data
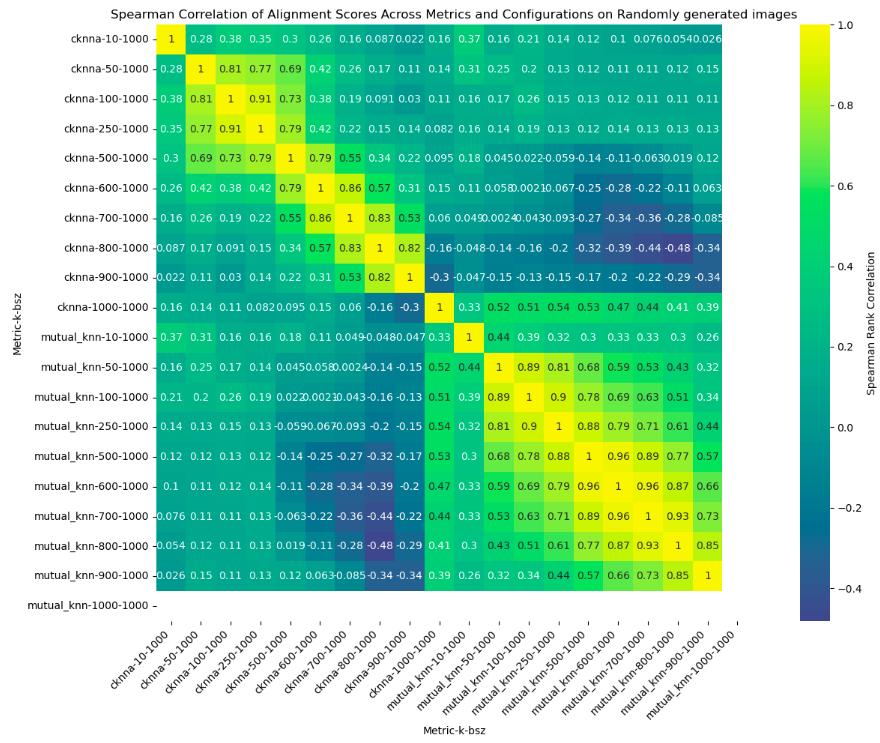
Figure 3: Spearman correlation of alignment scores on random noise data. The lower correlation values indicate a breakdown in representational alignment, suggesting that random data lacks the underlying structure required for PRH. This means that PRH is not just a random occurance but requires some statistical-structure to be present.
Discussion
When I first came across the PRH paper, my initial hypothesis was that PRH might be primarily due to the high similarity in training datasets, since most LLMs/LVMs are trained on extremely large datasets from common sources (ImageNet, Pile, etc.). However, the OOD experiments proved that this phenomenon of shared statistical structure generalizes well beyond the training distribution of the models. Further experiments with purely random data demonstrated that this is not just a coincidence but rather reflects inherent statistical structures present in “useful” data across all modalities.
The code for experiments and analysis in this paper is available on GitHub here.